Critical

Paths

Solution

Naive approach

Critical nodes in a DAG are commonly known as dominators. Let's define $Dom(u)$ as the set of nodes that dominate node $u$.

The dominator of the starting node is itself. The set of dominators for any other node $u$ is the intersection of the set of dominators for all ancestors $p$ of node $u$.

The following code uses the above rucerrence.

Copy
#include <bits/stdc++.h>

using namespace std;

const int NMAX = 1e5;

int n, m;
vector<int> g[NMAX];
vector<bitset<NMAX>> dom;
bool seen[NMAX];

Time complexity: $\mathcal{O}(N \cdot M)$.

Unfortunately, this is too slow.

A faster approach

In this approach we attempt building the dominator tree of the graph. A dominator tree is a tree where each node's children are thos nodes it immediately dominates. The start node is the root of the tree. The immediate dominator - or shortly idom - of a node $u$ is a node $v$ that strictly dominates node $u$ and every other dominator of node $u$ strictly dominates node $v$. The definition of the dominator tree gives us the following property: If node $v$ dominates node $u$, then node $v$ is an ancestor of node $u$, thus the answe of the problem is the path from the root to node $n$ in the dominator tree.

From now on, we'll discuss the construction of the dominator tree, but first we need to precompute some helpful values:

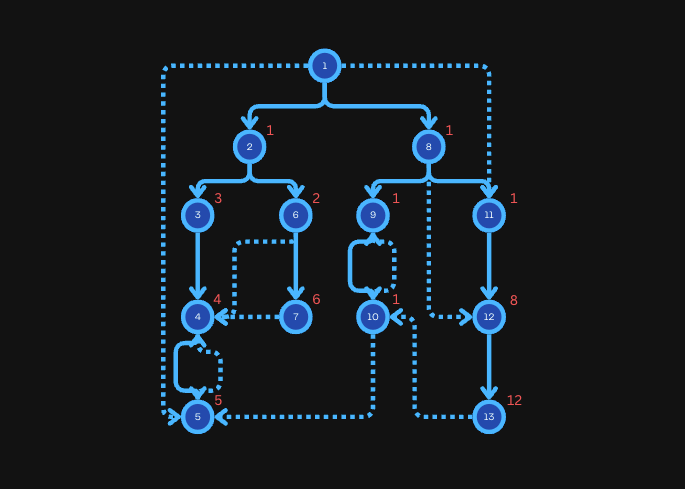
The following graph depicts the semi-dominator for every node. The full-color edges represent the edges part of the DFS tree.

Important properties

If you're interested in seeing proofs scroll down to the final section.

1. If $u \neq S$, then $sdom(u)$ is a proper ancestor of $u$ is the DFS tree.
2. If $u \neq S$, then idom(u) is an ancestor - not necessarily proper - of $u$ in the DFS tree.
3. Let $u \neq S$. If, for every vertex $x$ which is an ancestor of $u$ and has sdom(u) as its proper ancestor, $sdom(x) \geq sdom(u)$ then $idom(u)=sdom(u)$.
4. Let $w \neq S$. Let u be a vertex for which $sdom(u)$ is minimum among all vertices u satisfying “$sdom(w)$ is a proper ancestor of $u$ and $u$ is an ancestor of $w$”. If $sdom(u) \leq sdom(w)$ then $idom(w) = idom(u)$.
5. Let $u \neq S$ and &v& be a vertex for which $sdom(v)$ is minimum among all vertices $u$ satisfying: $sdom(u)$ is a proper ancestor of $v$ and $v$ is an ancestor of u. If $sdom(v) \le sdom(u)$ then $idom(u) = idom(v)$.
6. Let $w \neq S$. Let $u$ be a vertex for which $sdom(u)$ is minimum among all vertices $u$ satisfying “$sdom(w)$ is a proper ancestor of $u$ and $u$ is an ancestor of $w$”. Then:

Precompute Sdom

The following identity enables us the compute $sdom$:

In other words, $sdom(u)$ is the minimum node in the intersection of the following groups:

1. All the nodes $y$ with $y \le u \text{ and } (y,u) \in E$
2. $sdom(x)$ where $x > u \text{ and } (u, y) \in E$

Implementation

1. Precompute using a DFS the new mapping of the tree, i.e. the new labels of the nodes are their entry time $u = e[u]$.

2. Compute $sdom$ for all nodes by applying the formula mentioned in the previous section. Iterate over node in decreasing order, maintaining the visited nodes in a DSU. Also, the DSU is slightly modified:

• $Find(u)$ = Let $x$ be the root of the components

  • If $u=x$, return $x$;
  • else return a node $v$ with minimum sdom, lying on path from $u$ to $x$.

In order to process node $u$ we iterate over all incoming edges $(v, u):$

• If $v < u$, $v$ is an ancestor of $u$, $v$ would not have been processed till now, thus $Find(v)$ would return v.
• If $v > w$ then $v$ would have already been processed and $Find(v)$ would return a node $x$ lying on the path from $v$ to root in the DSU tree having minimum sdom.

The 2 cases cover precisely the definition $(2)$.

3. Compute the $idom$ for all nodes by applying $(1)$.

In this step, store nodes in buckets of their own $sdom$ and iterate over them updating the $idom$ value using $(1)$.

This snippet of code combines steps $2$ and $3$:

Copy
// Iterate decreasingly
for (int i = n - 1; i >= 0; i--) {
	// Iterat over incoming edges applying (2)
	for (int p : rg[i]) { sdom[i] = min(sdom[i], sdom[Find(p, 0)]); }
	// Insert i into it's bucket after sdom[i]
	if (i > 0) { bucket[sdom[i]].push_back(i); }
	// Apply (1) for nodes in bucket
	for (int node : bucket[i]) {
		int p = Find(node, 0);
		if (sdom[p] == sdom[node]) {

4. After steps $2$ and $3$, the $idom$ value has been set ($=sdom$), for every node $u$, or it has been set to an ancestor $v$ of $u$ and $idom(u)=idom(v)$. Now if we start processing nodes after (0) increasingly, then for any vertex $u$:

Copy
#include <functional>
#include <iostream>
#include <set>
#include <stack>
#include <vector>

using namespace std;

int main() {
	int n, m;

Time complexity: $\mathcal{O}((N+M) \cdot \log{N})$

Proofs

Cycles

• GP of Wroclaw 2020 H
• The Meeting Place Cannot be Changed
• USACO Camp - Acyclic Graphs